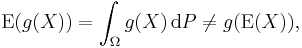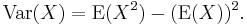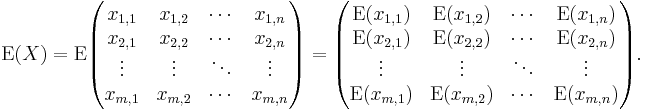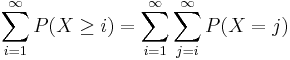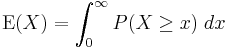Expected value
In probability theory and statistics, the expected value (or expectation value, or mathematical expectation, or mean, or first moment) of a random variable is the integral of the random variable with respect to its probability measure.[1][2]
For discrete random variables this is equivalent to the probability-weighted sum of the possible values.
For continuous random variables with a density function it is the probability density-weighted integral of the possible values.
The term "expected value" can be misleading. It must not be confused with the "most probable value." The expected value is in general not a typical value that the random variable can take on. It is often helpful to interpret the expected value of a random variable as the long-run average value of the variable over many independent repetitions of an experiment.
The expected value may be intuitively understood by the law of large numbers: The expected value, when it exists, is almost surely the limit of the sample mean as sample size grows to infinity. The value may not be expected in the general sense — the "expected value" itself may be unlikely or even impossible (such as having 2.5 children), just like the sample mean.
The expected value does not exist for some distributions with large "tails", such as the Cauchy distribution.[3]
It is possible to construct an expected value equal to the probability of an event by taking the expectation of an indicator function that is one if the event has occurred and zero otherwise. This relationship can be used to translate properties of expected values into properties of probabilities, e.g. using the law of large numbers to justify estimating probabilities by frequencies.
Contents |
History
The idea of the expected value originated in the middle of the 17th century from the study of the so-called problem of points, posed by a French nobleman chevalier de Méré. The problem was that of two players who want to finish a game early and, given the current circumstances of the game, want to divide the stakes fairly, based on the chance each has of winning the game from that point. This problem was solved in 1654 by Blaise Pascal in his private correspondence with Pierre de Fermat, however the idea was not communicated to the broad scientific community. Three years later, in 1657, a Dutch mathematician Christiaan Huygens published a treatise (see Huygens (1657)) “De ratiociniis in ludo aleæ” on probability theory, which not only lay down the foundations of the theory of probability, but also considered the problem of points, presenting a solution essentially the same as Pascal’s. [4]
Neither Pascal nor Huygens used the term “expectation” in its modern sense. In particular, Huygens writes: “That my Chance or Expectation to win any thing is worth just such a Sum, as wou’d procure me in the same Chance and Expectation at a fair Lay. … If I expect a or b, and have an equal Chance of gaining them, my Expectation is worth  .” More than a hundred years later, in 1814, Pierre-Simon Laplace published his tract “Théorie analytique des probabilités”, where the concept of expected value was defined explicitly:
.” More than a hundred years later, in 1814, Pierre-Simon Laplace published his tract “Théorie analytique des probabilités”, where the concept of expected value was defined explicitly:
| “ | … This advantage in the theory of chance is the product of the sum hoped for by the probability of obtaining it; it is the partial sum which ought to result when we do not wish to run the risks of the event in supposing that the division is made proportional to the probabilities. This division is the only equitable one when all strange circumstances are eliminated; because an equal degree of probability gives an equal right for the sum hoped for. We will call this advantage mathematical hope. | ” |
The use of letter E to denote expected value goes back to W.A. Whitworth (1901) “Choice and chance”. The symbol has become popular since for English writers it meant “Expectation”, for Germans “Erwartungswert”, and for French “Espérance mathématique”.[5]
Examples
The expected outcome from one roll of an ordinary (that is, fair) six-sided die is
which is not among the possible outcomes.[6]
A common application of expected value is gambling. For example, an American roulette wheel has 38 places where the ball may land, all equally likely. A winning bet on a single number pays 35-to-1, meaning that the original stake is not lost, and 35 times that amount is won, so you receive 36 times what you've bet. Considering all 38 possible outcomes, the expected value of the profit resulting from a dollar bet on a single number is the sum of potential net loss times the probability of losing and potential net gain times the probability of winning, that is,
The net change in your financial holdings is −$1 when you lose, and $35 when you win. Thus one may expect, on average, to lose about five cents for every dollar bet, and the expected value of a one-dollar bet is $0.947368421. In gambling, an event of which the expected value equals the stake (i.e. the bettor's expected profit, or net gain, is zero) is called a “fair game”.
Mathematical definition
In general, if 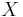 is a random variable defined on a probability space
is a random variable defined on a probability space  , then the expected value of
, then the expected value of 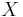 , denoted by
, denoted by 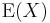 ,
, 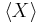 ,
, 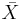 or
or 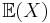 , is defined as
, is defined as
When this integral converges absolutely,it is called the expectation of X.The absolute convergence is necessary because conditional convergence means that different order of addition gives different result,which is against the nature of expected value. Here the Lebesgue integral is employed. Note that not all random variables have an expected value, since the integral may not converge absolutely (e.g., Cauchy distribution). Two variables with the same probability distribution will have the same expected value, if it is defined.
If  is a discrete random variable with probability mass function
is a discrete random variable with probability mass function  , then the expected value becomes
, then the expected value becomes
as in the gambling example mentioned above.
If the probability distribution of  admits a probability density function
admits a probability density function  , then the expected value can be computed as
, then the expected value can be computed as
It follows directly from the discrete case definition that if  is a constant random variable, i.e.
is a constant random variable, i.e. 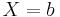 for some fixed real number
for some fixed real number  , then the expected value of
, then the expected value of  is also
is also  .
.
The expected value of an arbitrary function of X, g(X), with respect to the probability density function f(x) is given by the inner product of f and g:
This is sometimes called the law of the unconscious statistician. Using representations as Riemann–Stieltjes integral and integration by parts the formula can be restated as
 if
if 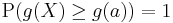 ,
,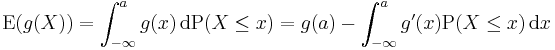 if
if 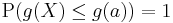 .
.
As a special case let 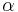 denote a positive real number, then
denote a positive real number, then
In particular, for  , this reduces to:
, this reduces to:
if ![P[X \ge 0]=1](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/8480e6201fb77890d87e12f903a2f77c.png) , where F is the cumulative distribution function of X.
, where F is the cumulative distribution function of X.
Conventional terminology
- When one speaks of the "expected price", "expected height", etc. one means the expected value of a random variable that is a price, a height, etc.
- When one speaks of the "expected number of attempts needed to get one successful attempt," one might conservatively approximate it as the reciprocal of the probability of success for such an attempt. Cf. expected value of the geometric distribution.
2e-83
Properties
Constants
The expected value of a constant is equal to the constant itself; i.e., if c is a constant, then 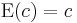 .
.
Monotonicity
If X and Y are random variables so that 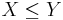 almost surely, then
almost surely, then 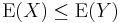 .
.
Linearity
The expected value operator (or expectation operator) 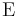 is linear in the sense that
is linear in the sense that
Note that the second result is valid even if X is not statistically independent of Y. Combining the results from previous three equations, we can see that
for any two random variables  and
and  (which need to be defined on the same probability space) and any real numbers
(which need to be defined on the same probability space) and any real numbers 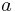 and
and  .
.
Iterated expectation
Iterated expectation for discrete random variables
For any two discrete random variables 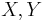 one may define the conditional expectation:[7]
one may define the conditional expectation:[7]
which means that  is a function on
is a function on 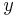 .
.
Then the expectation of  satisfies
satisfies
Hence, the following equation holds:[8]
The right hand side of this equation is referred to as the iterated expectation and is also sometimes called the tower rule. This proposition is treated in law of total expectation.
Iterated expectation for continuous random variables
In the continuous case, the results are completely analogous. The definition of conditional expectation would use inequalities, density functions, and integrals to replace equalities, mass functions, and summations, respectively. However, the main result still holds:
Inequality
If a random variable X is always less than or equal to another random variable Y, the expectation of X is less than or equal to that of Y:
If 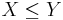 , then
, then 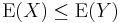 .
.
In particular, since 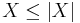 and
and  , the absolute value of expectation of a random variable is less than or equal to the expectation of its absolute value:
, the absolute value of expectation of a random variable is less than or equal to the expectation of its absolute value:
Non-multiplicativity
In general, the expected value operator is not multiplicative, i.e.  is not necessarily equal to
is not necessarily equal to 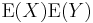 . If multiplicativity occurs, the
. If multiplicativity occurs, the  and
and  variables are said to be uncorrelated (independent variables are a notable case of uncorrelated variables). The lack of multiplicativity gives rise to study of covariance and correlation.
variables are said to be uncorrelated (independent variables are a notable case of uncorrelated variables). The lack of multiplicativity gives rise to study of covariance and correlation.
If one considers the joint PDF of X and Y, say j(X,Y), then the expectation of XY is
Now if X and Y are independent, then by definition j(X,Y)=f(X)g(Y) where f and g are the marginal PDFs for X and Y. Then
Observe that independence of X and Y is required only to write j(X,Y)=f(X)g(Y), and this is required to establish the third equality above.
Functional non-invariance
In general, the expectation operator and functions of random variables do not commute; that is
A notable inequality concerning this topic is Jensen's inequality, involving expected values of convex (or concave) functions.
Uses and applications
The expected values of the powers of  are called the moments of
are called the moments of  ; the moments about the mean of
; the moments about the mean of  are expected values of powers of
are expected values of powers of  . The moments of some random variables can be used to specify their distributions, via their moment generating functions.
. The moments of some random variables can be used to specify their distributions, via their moment generating functions.
To empirically estimate the expected value of a random variable, one repeatedly measures observations of the variable and computes the arithmetic mean of the results. If the expected value exists, this procedure estimates the true expected value in an unbiased manner and has the property of minimizing the sum of the squares of the residuals (the sum of the squared differences between the observations and the estimate). The law of large numbers demonstrates (under fairly mild conditions) that, as the size of the sample gets larger, the variance of this estimate gets smaller.
In classical mechanics, the center of mass is an analogous concept to expectation. For example, suppose  is a discrete random variable with values
is a discrete random variable with values  and corresponding probabilities
and corresponding probabilities  . Now consider a weightless rod on which are placed weights, at locations
. Now consider a weightless rod on which are placed weights, at locations  along the rod and having masses
along the rod and having masses  (whose sum is one). The point at which the rod balances is
(whose sum is one). The point at which the rod balances is 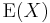 .
.
Expected values can also be used to compute the variance, by means of the computational formula for the variance
A very important application of the expectation value is in the field of quantum mechanics. The expectation value of a quantum mechanical operator 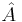 operating on a quantum state vector
operating on a quantum state vector 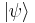 is written as
is written as 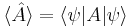 . The uncertainty in
. The uncertainty in 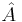 can be calculated using the formula
can be calculated using the formula 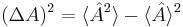 .
.
Expectation of matrices
If  is an
is an 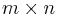 matrix, then the expected value of the matrix is defined as the matrix of expected values:
matrix, then the expected value of the matrix is defined as the matrix of expected values:
This is utilized in covariance matrices.
Formulas for special cases
Discrete distribution taking only non-negative integer values
When a random variable takes only values in  we can use the following formula for computing its expectation:
we can use the following formula for computing its expectation:
Proof:
interchanging the order of summation, we have
as claimed. This result can be a useful computational shortcut. For example, suppose we toss a coin where the probability of heads is  . How many tosses can we expect until the first heads (not including the heads itself)? Let
. How many tosses can we expect until the first heads (not including the heads itself)? Let  be this number. Note that we are counting only the tails and not the heads which ends the experiment; in particular, we can have
be this number. Note that we are counting only the tails and not the heads which ends the experiment; in particular, we can have 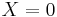 . The expectation of
. The expectation of  may be computed by
may be computed by 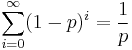 . This is because the number of tosses is at least
. This is because the number of tosses is at least  exactly when the first
exactly when the first  tosses yielded tails. This matches the expectation of a random variable with an Exponential distribution. We used the formula for Geometric progression:
tosses yielded tails. This matches the expectation of a random variable with an Exponential distribution. We used the formula for Geometric progression: 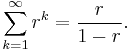
Continuous distribution taking non-negative values
Analogously with the discrete case above, when a continuous random variable X takes only non-negative values, we can use the following formula for computing its expectation:
Proof: It is first assumed that X has a density 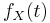 .
.
interchanging the order of integration, we have
as claimed. In case no density exists, it is seen that 
See also
- Conditional expectation
- An inequality on location and scale parameters
- Expected value is also a key concept in economics, finance, and many other subjects
- The general term expectation
- Moment (mathematics)
- Expectation value (quantum mechanics)
- Wald's equation for calculating the expected value of a random number of random variables
Notes
- ↑ Sheldon M Ross (2007). "§2.4 Expectation of a random variable". Introduction to probability models (9th ed.). Academic Press. p. 38 ff. ISBN 0125980620. http://books.google.com/books?id=12Pk5zZFirEC&pg=PA38.
- ↑ Richard W Hamming (1991). "§2.5 Random variables, mean and the expected value". The art of probability for scientists and engineers. Addison-Wesley. p. 64 ff. ISBN 0201406861. http://books.google.com/books?id=jX_F-77TA3gC&pg=PA64.
- ↑ For a discussion of the Cauchy distribution, see Richard W Hamming (1991). "Example 8.7–1 The Cauchy distribution". The art of probability for scientists and engineers. Addison-Wesley. p. 290 ff. ISBN 0201406861. http://books.google.com/books?id=jX_F-77TA3gC&printsec=frontcover&dq=isbn:0201406861&cd=1#v=onepage&q=Cauchy&f=false. "Sampling from the Cauchy distribution and averaging gets you nowhere – one sample has the same distribution as the average of 1000 samples!"
- ↑ In the foreword to his book, Huygens writes: “It should be said, also, that for some time some of the best mathematicians of France have occupied themselves with this kind of calculus so that no one should attribute to me the honour of the first invention. This does not belong to me. But these savants, although they put each other to the test by proposing to each other many questions difficult to solve, have hidden their methods. I have had therefore to examine and go deeply for myself into this matter by beginning with the elements, and it is impossible for me for this reason to affirm that I have even started from the same principle. But finally I have found that my answers in many cases do not differ from theirs.” (cited in Edwards (2002)). Thus, Huygens learned about de Méré’s problem in 1655 during his visit to France; later on in 1656 from his correspondence with Carcavi he learned that his method was essentially the same as Pascal’s; so that before his book went to press in 1657 he knew about Pascal’s priority in this subject.
- ↑ "Earliest uses of symbols in probability and statistics". http://jeff560.tripod.com/stat.html.
- ↑ Sheldon M Ross. "Example 2.15". cited work. p. 39. ISBN 0125980620. http://books.google.com/books?id=12Pk5zZFirEC&pg=PA39.
- ↑ Sheldon M Ross. "Chapter 3: Conditional probability and conditional expectation". cited work. p. 97 ff. ISBN 0125980620. http://books.google.com/books?id=12Pk5zZFirEC&pg=PA97.
- ↑ Sheldon M Ross. "§3.4: Computing expectations by conditioning". cited work. p. 105 ff. ISBN 0125980620. http://books.google.com/books?id=12Pk5zZFirEC&pg=PA105.
Historical background
External links
- An 8 foot tall Probability Machine (named Sir Francis) comparing stock market returns to the randomness of the beans dropping through the quincunx pattern. from Index Funds Advisors IFA.com, youtube.com
- Expectation on PlanetMath
|
|||||||||||||
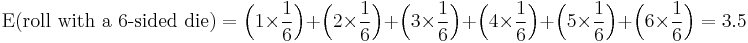
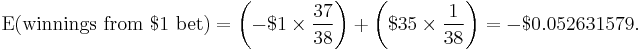
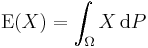


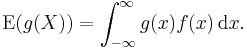
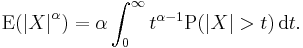
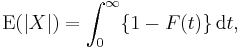

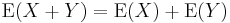


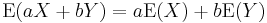
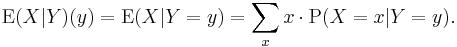
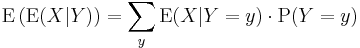

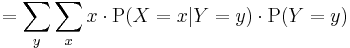
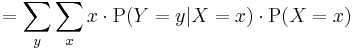


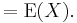

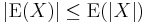
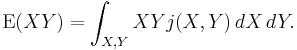
![\begin{align}
\operatorname{E}(XY) & = \int_{X,Y}XYf(X)g(Y)\,dX\,dY=
\int_X\int_Y XYf(X)g(Y)\,dX\,dY \\
& = \int_X Xf(X)\left[\int Yg(Y)\,dY\right]\,dX=\int_XXf(X)\operatorname{E}(Y)\,dX=\operatorname{E}(X)\operatorname{E}(Y)
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b0c0995cab43d94f814086ef038b667a.png)